A Realistic Look at Quantum Computing
With a side of reversible computing
There has been significant hype around Quantum Computing over the past few years. While there certainly are a lot of interesting ideas in the space, especially in terms of mathematics, enormous engineering hurdles that are not clearly solvable stand in the way of practical quantum computers.
While much skepticism has been pointed in the past at efforts to overcome decoherence and error in quantum computers, I’d like to point my critique elsewhere. Even if we assume that quantum computers can overcome every engineering challenge that currently exists (which in my opinion is still an enormous if), even perfect quantum computers have a variety of other serious limitations that are only rarely discussed.
In short, while quantum computers may be theoretically exponentially faster than classical computers in some cases, there are also many other cases where they are exponentially slower, and even some notable examples of trivial problems for classical computers that arguably are not possible for quantum computers to solve at all.
Luckily, most of these do not actually require much understanding of quantum properties, only the reversible nature of quantum systems and some properties of wave function collapse.
Quantum Reversibility
One fundamental property of quantum systems is time-reversibility; quantum information is always conserved (unless maybe if you’re near a black hole).
Quantum information is never truly lost, at worst it is only ever leaked into an external environment we are not measuring. In principle, if we know the wave function of a quantum system, we should be able to compute its state arbitrarily far into the past or future, at least up until it interacts with some external system we are not modeling (including ourselves, which would occur during measurement).
A consequence of this is that quantum computers are by necessity a type of reversible computer.
Reversible computers are theoretically a very interesting kind of computer, where all operations have the same number of inputs as outputs and no information is ever lost - given the output of an operation, the original input can always be reconstructed.
Reversible computers are also potentially practically very interesting due to their potential ability to bypass Landauer’s Limit and allow arbitrarily efficient computation, so long as it conforms to the constraints of a reversible computer. This may sound great - extremely efficient computation! However, these reversibility constraints are very tight, and many types of computation we care about are not reversible, limiting exactly how useful such computers can be in practice.
Reversible Gates
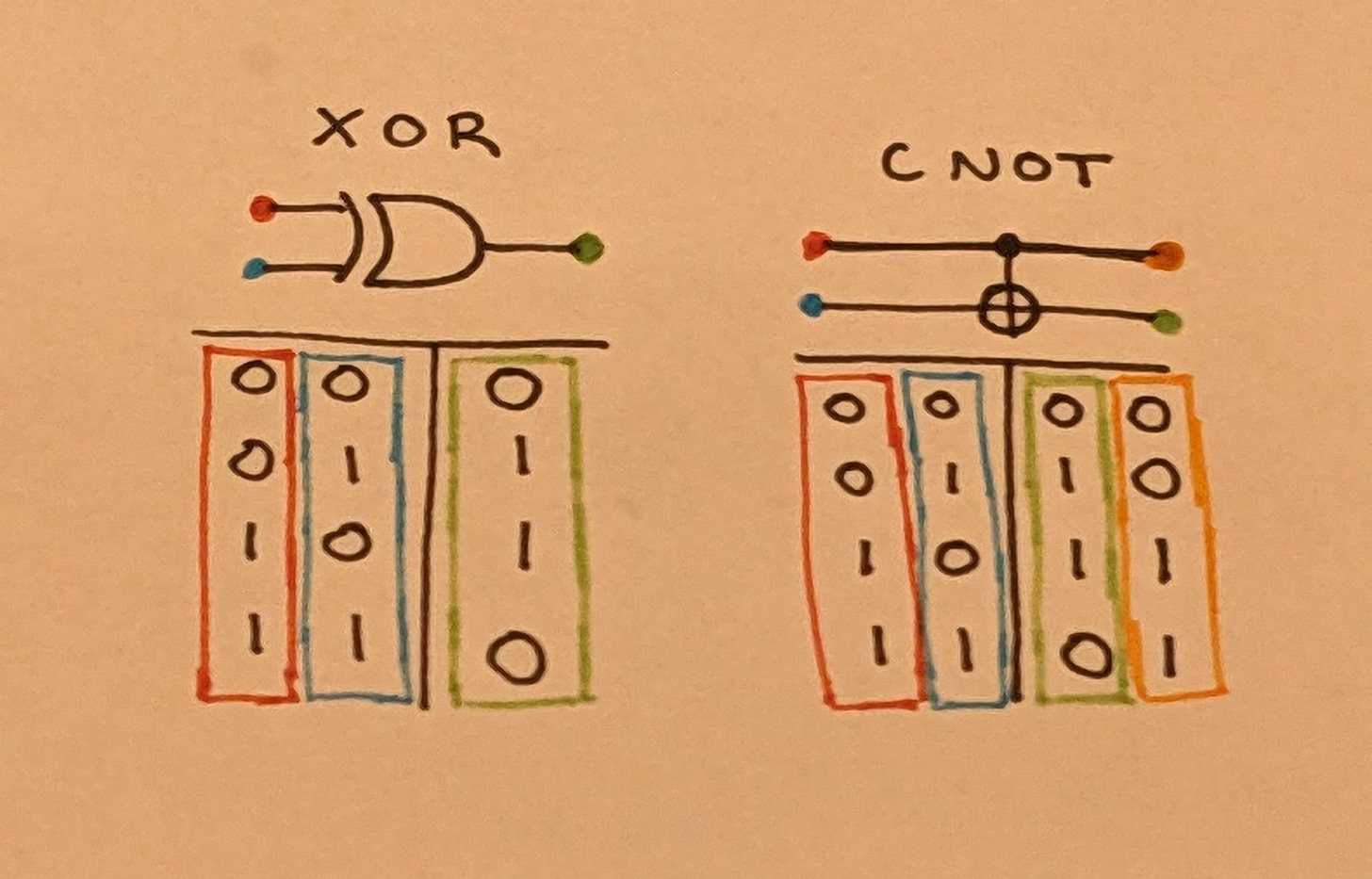
In traditional computing, the standard logic gates are AND, OR, and NOT, with sometimes other gates like NAND, NOR, XOR, and XNOR being mentioned as well. All familiar computations can be reduced to some circuit composed of these gates.
In order for a gate to be reversible, it must have the same number of inputs as outputs. If we’re looking for reversible classical gates, the only one that fits this criteria is NOT. NOT is in fact a reversible gate - if the output is 1, you know the input was 0, and vice-versa.
Say we wanted to create reversible versions of the other gates. Let’s start out with XOR, because it’s the simplest to adapt. First, we need to have the same number of outputs as inputs, so our reversible XOR gate will have 2 inputs and 2 outputs.
In classical computation, every input to a circuit has exactly one possible output. This is also true for reversible computation, however with the addition of a second property, which is that for every possible output, we have exactly one corresponding input. We cannot have situations where two input states map to the exact same output state.
Side note: For those wondering about what happens when you enforce neither of these properties, the answer is that you get NP computation.
In order to design our reversible XOR gate we must decide the truth table for its second output while making sure that it fits both of these properties. Both of these properties together implies that a reversible computation is what mathematicians call a bijection - a one-to-one mapping, in this case between the input truth table and the output truth table.
There are in fact only two ways to accomplish this, both of which amount to simply setting this additional output to be equal to one of the inputs. Overall, the behavior of this reversible XOR gate is to take two inputs and return both, but with the one flipped if the other is a 1. The name for this new gate is CNOT, or a controlled NOT gate.
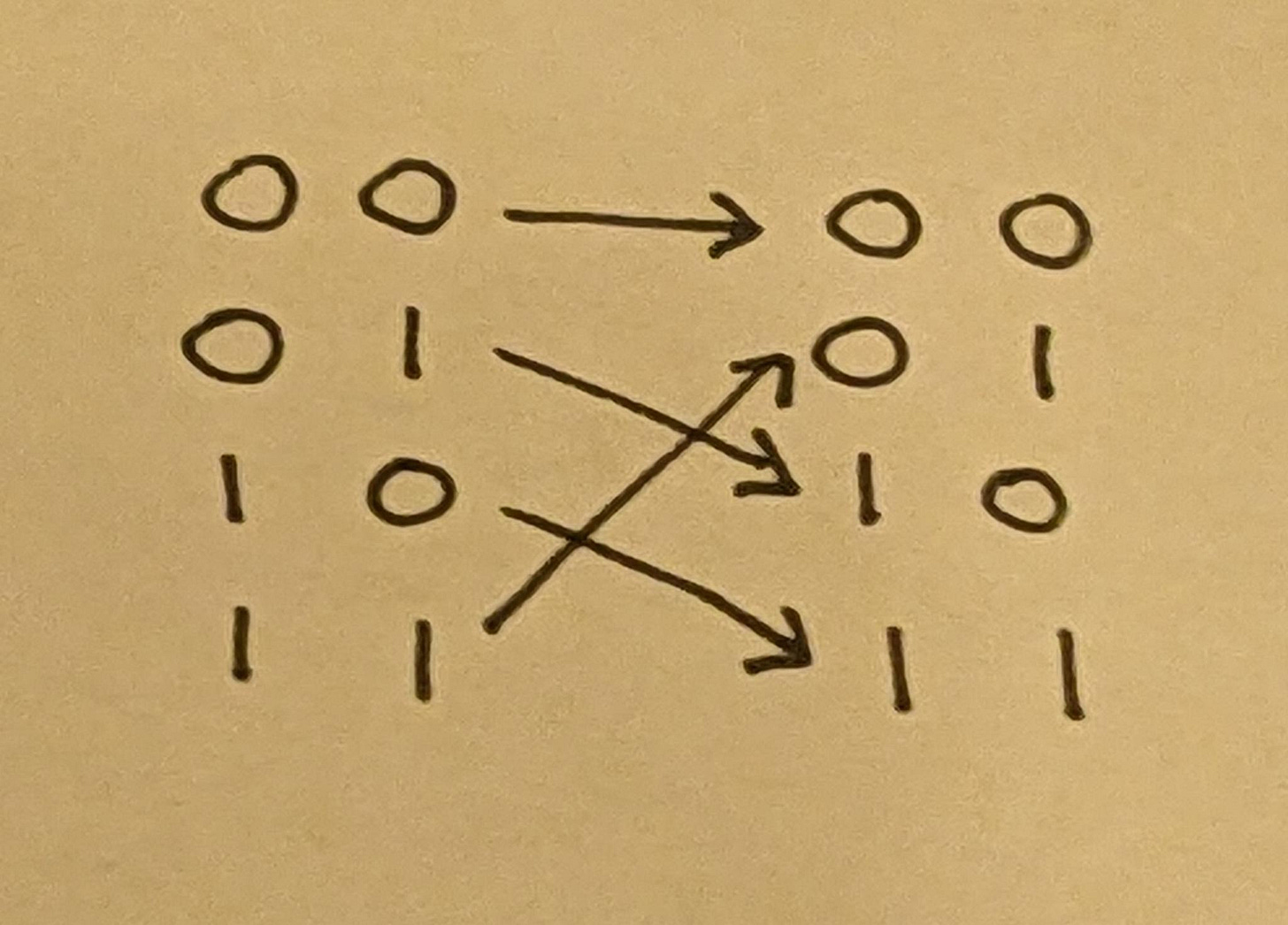
We can also verify that the bijection property holds:
This additional output, if we are unable to make use of it, is called an ancilla bit, and is effectively a waste product. From a thermodynamic perspective, ancilla bits can be thought of as encoding the entropy that we would otherwise leak into the external environment in the form of waste heat. We then have the opportunity to reuse it for future work rather than simply losing it, saving energy.
A CNOT gate interestingly has the property that, assuming the modified bit is known to be zero beforehand, we are able to duplicate the unmodified bit, making this the primary operation for moving memory.
Let’s look at another example; an AND gate. This is a more complex situation.
If we look at the set of possible states for any given combination of bits, we find that for any chosen bit, half of those states will have that bit set to 0 and half will have it set to 1. In the case of an AND gate, our primary output bit has three states where it is 0 and one where it is 1. It is impossible to map this onto a 2-bit state space.
The solution to this is that we can add a third input/output to our gate that we assume will always be zero. Reversible computations usually include a number of additional input bits initialized to zero to make operations like this easier, as well as to provide a “working memory”.
There are many ways we can do this, but one simple approach would be to use the third input as an output. In this case, we flip the third input if the first two inputs are both 1, with the first two inputs both being returned unchanged.
This is commonly called a CCNOT gate (controlled-controlled-NOT), also called a Toffoli gate.
There are plenty of other reversible gates as well, with a couple common ones being SWAP and CSWAP (also called Fredkin). Toffoli and Fredkin gates are both universal gates, and any other reversible circuit can be constructed entirely from either all Toffoli gates or all Fredkin gates.
(Note: there is no “universal gate” in quantum computing, as the gates required for adding purely quantum operations create additional complexities. Instead, multiple different kinds of gates are involved, with Toffoli/Fredkin gates handling some things, other gates handling qubit phase shifts, and others handling things like superposition, entaglement, and measurement.)
Reversible computer circuits are often drawn as a collection of lines, each representing one bit (or in this diagram, qubits). Gates usually take the form of vertical lines with symbols for each bit they operate on.
Ancilla bits can be hard to get rid of. Often, we can “uncompute” them by copying the result elsewhere and then running the computation in reverse (a simple example of which is demonstrated in the above diagram). There are of course limitations to this - if any of the original inputs of a function are still in use, or if any of the original inputs that were used to compute those inputs are still in use, etc., we can only uncompute back so far. The maximum extent of uncomputation leaves us with just the initial input, past which uncomputation ceases to have any meaning.
While perhaps useful on an ordinary reversible computer, quantum computers make uncomputation more difficult thanks to errors and superpositions making it even harder to reliably reconstruct the original input.
Any ancilla bits that we cannot get rid of are bits that we are stuck with for the duration of the computation, sometimes being referred to as “garbage”. Quantum computers especially only have a finite and typically small number of qubits, so garbage adds up fast. And no, aside from uncomputation there is no quantum garbage collector.
Hard Problems
There are some problems that are not easily practical for reversible computers.
One obvious question some readers might have is “what about cryptography?” If we run a cryptographic function on a reversible computer, it might appear as though we could extract any secret input values from the output by running the computation in reverse.
Where this logic breaks down is in finding the exact output for the reversible computer to reverse back into the original input. If we do not know the exact state of every output bit in a reversible computer, we cannot reconstruct the original input. In the example of a cryptographic function, we as an attacker have access to the main output value, but we lack all of the ancilla/garbage bits that were produced as a byproduct. Nothing changes if we assume that uncomputation was involved - uncomputing those ancilla bits merely returns those bits back to their original state, including that private key that we do not have and are trying to access.
As a review - reversible computers make traditionally non-reversible computations reversible by giving them additional outputs. However, without the exact values of those outputs we are unable to perform that reversal. Unless the person you’re trying to attack was dumb enough to post all of the ancilla bits - or even stupider their full private key - they’re perfectly safe from any attacks from your reversible computer.
Quantum computers may be a threat against some types of cryptography, but that’s a consequence of purely quantum operations that are not available in a classical reversible computer.
Another mild difficulty is control flow. For example, an if/else statement that decides which of two reversible circuits to apply based on a given bit.
If we have a way of extracting this condition variable from our program state and using it to decide which gates to apply next, our reversible computer should be able to implement efficient if/else statements. If not, we still have the option of evaluating both branches and then passing the results we care about onto futher computations while leaving the unwanted results as ancilla bits, maybe uncomputing them if possible.
While at first evaluating both sides of each branch may appear to only make our control-flow-heavy code roughly twice as slow, it gets worse if we have more than two possible paths a branch can take (e.g. switch statements), and has the opportunity to get exponentially worse if we have nested if/else statements, as occurs with some recursive search algorithms.
While reading out bits to affect control flow shouldn’t be a big deal for a classical reversible computer, this would create a problem for a quantum computer - the system that decides which quantum gates to apply to your qubits next is a classical computer independent from your quantum state. Reading even a single qubit to check such a condition value would (at least partially) collapse the wave function, diminishing the power of your quantum computer and likely destroying a lot of the complex quantum state that you’ve worked so hard to build.
If you don’t plan on destroying much of your quantum advantage, your best option on a quantum computer is to simply take the slower option, evaluating every forking path of control flow and ignoring any results you don’t need, no matter how many qubits that eats up.
With regards to RAM, I haven’t heard much about reversible RAM or quantum RAM, and from my understanding doing this properly requires essentially a very large number of bits and lots of different gates for conditionally shuffling bits around. Each random memory access is basically a big switch statement, each case operating on a different variable.
I’m not sure how exactly bad it would be for a reversible computer; at the very least, being a classical computer it could fall back on traditional memory technologies when willing to pay the energy cost. A quantum computer however is an entirely different beast. There is no possibility for quantum I/O while maintaining the wave function, so any external memory storage is off the table. The quantum state is thus limited to whatever maximum number of qubits can be stored entirely in the quantum computer. Quantum random memory access would require very large numbers of gates, as every memory operation would be the equivalent of a giant switch statement but without any optimizations that a non-quantum computer might permit.
I have found some research into quantum data structures, but the purely quantum ones are extremely simple and mostly rely on just slamming Grover’s Algorithm into large numbers of qubits rather than anything that would actually make good use of random memory access.
It seems there probably won’t be much in terms of efficient quantum data structures without some major theoretical breakthroughs, if ever at all.
Quantum Impossibility
If not being able to read qubits for quantum branches is bad, it’s nothing compared to not being able to run quantum loops.
A for loop might not be too bad, at least when the exact number of iterations is known at compile time. However, a quantum computer faced with a loop without a clear maximum number of iterations simply has no way of ever reliably exiting the loop.
For a quantum computer, all while loops are infinite loops, and all best-case runtimes are identical to worst-case runtimes.
Granted, there is some flexibility here - it is possible to only partially collapse a wave function if the qubits you’re collapsing are only weakly entangled with the quantum state you care about preserving. This is effectively how quantum error correcting codes work. I’m sure this opens up a little wiggle room for flexible running times, but undoubtedly most nontrivial problems are still off the table.
Quantum Realism
Even if all of the hard engineering problems with quantum computers can be solved - if noise can be reduced, if error-correcting codes can be scaled, and if quantum bits and gates can be made reliable enough to not skew results over long computations, the lack of efficient if/else statements, while loops, and RAM appear to be harsh enough constraints to kill off a wide range of potential applications.
One commonly heralded application of quantum computers is in more precisely solving hard combinatorial and optimization problems. For cryptographic algorithms, this might be a problem. Then again, quantum circuits for breaking such algorithms often require billions if not trillions of gates at a minimum, and enormous engineering challenges lay ahead for anyone who intends to maintain a quantum state for a computation that long.
Grover’s algorithm might be able to bring some O(2^N) problems down to O(2^(N/2)) time. This is theoretically an improvement, but it’s still exponential time, and as far as algorithmic speedups on exponential time go, it’s pretty lame compared to classical techniques.
If you care about the Travelling Salesman Problem (TSP) for example, or any problem that can be translated into it, the Christofides algorithm can actually find an approximate solution in polynomial time. The solutions it finds tend to be only about 10% worse than optimal on average, and it has been proven that it will never produce a solution more than 50% worse than optimal. That’s extremely good for such a notoriously hard optimization problem, but if that’s still not good enough for you, local search techniques can always be used to try to find even more optimal solutions. While they may not be guaranteed to converge onto an optimal solution, they get closer and closer the longer you wait.
In practice, perfectly optimal solutions to the TSP have extremely few if any real-world applications, and investing billions into quantum computers to replace our fast approximate algorithms with a slow quantum algorithm that produces results only a couple percent better probably isn’t worth it for any application.
Or for another hard, common, combinatorial problem, look at Boolean Satisfiability Problems (SAT). The difference between average-case and worst-case performance of SAT solvers is often extraordinary - a random SAT problem with a few hundred variables might be impractical to compute a solution for, but a “real world SAT problem” with a million variables might be reliably solved within an hour. There is an enormous gap here between theory and practice (particularly around the lack of any formal definition of “real world problems”), and this gap means that many exceptionally fast SAT solvers are difficult to describe in terms of their time complexity, lying in a blind spot of modern theoretical computer science.
If you know that the worst-case performance of your algorithm is exponentially slow, but finding any accurate way to describe your average-case performance is not only an unsolved problem, but is closely related to one of the most notorious unsolved problems in all of mathematics, it’s easy for some quantum researchers to spin something as slow as Grover’s algorithm as an improvement to investors and journalists.
Regardless, the best SAT solvers that do have proven lower bounds are typically between 1.333^N to 1.307^N, both of which are faster than the 1.414^N that Grover’s algorithm would require for SAT, while also depending on enough heavy use of while loops and if/else statements to likely rule out any possibility for any quantum versions.
Overall, I suspect that quantum computers will still be useful for simulating quantum systems, however for most other applications there will be few reasons to use them. Both classical and reversible computers still have enormous advantages, and most of the quantum advantages are much larger in theory than in practice.
Thank you for reading this week’s article. I’m trying to do some more technical writing again, though these take more time and I’m starting a new job tomorrow which will complicate my schedule. There is a chance I might change my substack schedule eventually to try to publish one longer, higher-quality article every two weeks rather than each week. I’m not sure about that yet though.