Neural Computing pt 1: Sparse Distributed Memory
There’s a great deal that we should be able to learn from neuroscience. The brain clearly computes in a way that is very alien to how human-engineered computers work, and it produces very alien results; a kind of intelligence that we currently struggle to replicate with any technology currently known.
Of course, neuroscience currently lacks any detailed, solid theory of brain function. That does not mean however that we can't get some valuable insights from piecing together what is known, and then extrapolating properties that such a system might have.
Deep learning has certainly gotten a lot of value out of some simplified models of neurons, synapses, and hierarchy in the brain, even if its versions of these ideas are extremely cartoonish compared to the real brain, and several other biologically unrealistic ideas like backpropagation need to be added to fill the gap between this product and practicality.
While there currently is no solid unified framework of how all of the brain works, many details are known that place tight constraints on what the brain may or may not be doing, and combinations of these details can offer some very interesting models. Several theoretical models exist for different parts of the brain, and I plan to explore over a series of articles a few of the ones that I find particularly interesting. These models of course also carry many caveats that suggest that the reality is more complex and strange, but having a flawed place to start is far superior than having no place to start at all. No theory materializes fully-formed.
Perhaps we can think of these models as being a bit like theories of physics; general relativity and quantum mechanics are both profoundly accurate and useful models of reality in their own right, but attempts so far to unify them into a single model have failed. Further, there are phenomena such as dark matter and dark energy that are currently observed, but completely unexplained by these theories. Then there are other details - such as there being three generations of matter - that are fairly easy to model in terms of their behavior, but that seem to imply underlying mechanisms we don't yet understand.
There are good reasons to look to the brain for computing ideas. The most obvious one is that general intelligence seems like a practically useful tool to bring into our engineering. There’s also all the pattern recognition applications that DL has been helping us with. Beyond that though, the brain seems particularly good at computing in extremely noisy environments, to an extent that even our deep learning models often aren't great at handling.
Then there is of course broader societal benefits beyond computing; a much deeper understanding of how humans think would likely be very valuable in fields such as psychology, economics, and politics. It would be very useful to counter mental disorders in a way that is much more precise than poorly-understood medications, perhaps being able to trace subtle details in how culture and environments contribute to mass psychosis. Precise social reform seems to be a much better option than mass medication if we can learn enough to pull it off.
In this first article on brain computing, I'd like to explore a model that dates back to the 80s called Sparse Distributed Memory, developed by Pentti Kanerva. It is a model that has many flaws and oversimplifies things a lot, but I find it to be a great introduction to some of the other models I'd like to explore in future articles.
Sparse Distributed Memory
SDM attempts to model the brain as a kind of addressing system, with many analogies made to computer memory. Each neuron can be thought of as something like a memory location, with the input to the brain region corresponding to an address. Unlike computer memory, there is nothing stored at a memory location and accessing a neuron's “address” just causes it to fire. Neuron outputs in SDM are binary; an active neuron outputs a 1 and an inactive neuron outputs a 0. Just as the input to a brain region in SDM is a bit vector, so is the output, with one bit for every neuron.
Each neuron in SDM has synapses, each with a numerical weight. The synapses receive inputs from other neurons. Whether a neuron fires or not is determined by checking if the sum of all of its synapses, weighted by each synapse's weight, exceeds a certain threshold.
To anyone familiar with machine learning, please note the all-or-nothing nonlinearity of the threshold function.
To anyone interested in the neuroscience, the particular way in which synapses work here is not very accurate, particularly involving negative weights; negative weight synapses do exist in the cortex, but do not seem directly capable of learning, nor can synapses switch the sign of their weight. Future articles in this series will discuss models that deal with this more accurately.
It's also worth noting that ordinary memory addressing can be seen as a special case of this operation. Given a 64-bit address space, we could think of each memory address as having a corresponding neuron with 64 synapses. Each neuron would encode a different 64-bit number, with zero bits represented by a -1 weight synapse and one bits represented by a +1 weight synapse. The threshold of each neuron can then be set to the sum of all of these, meaning that the only value that causes the neuron to fire is an exact match on the encoded binary address.
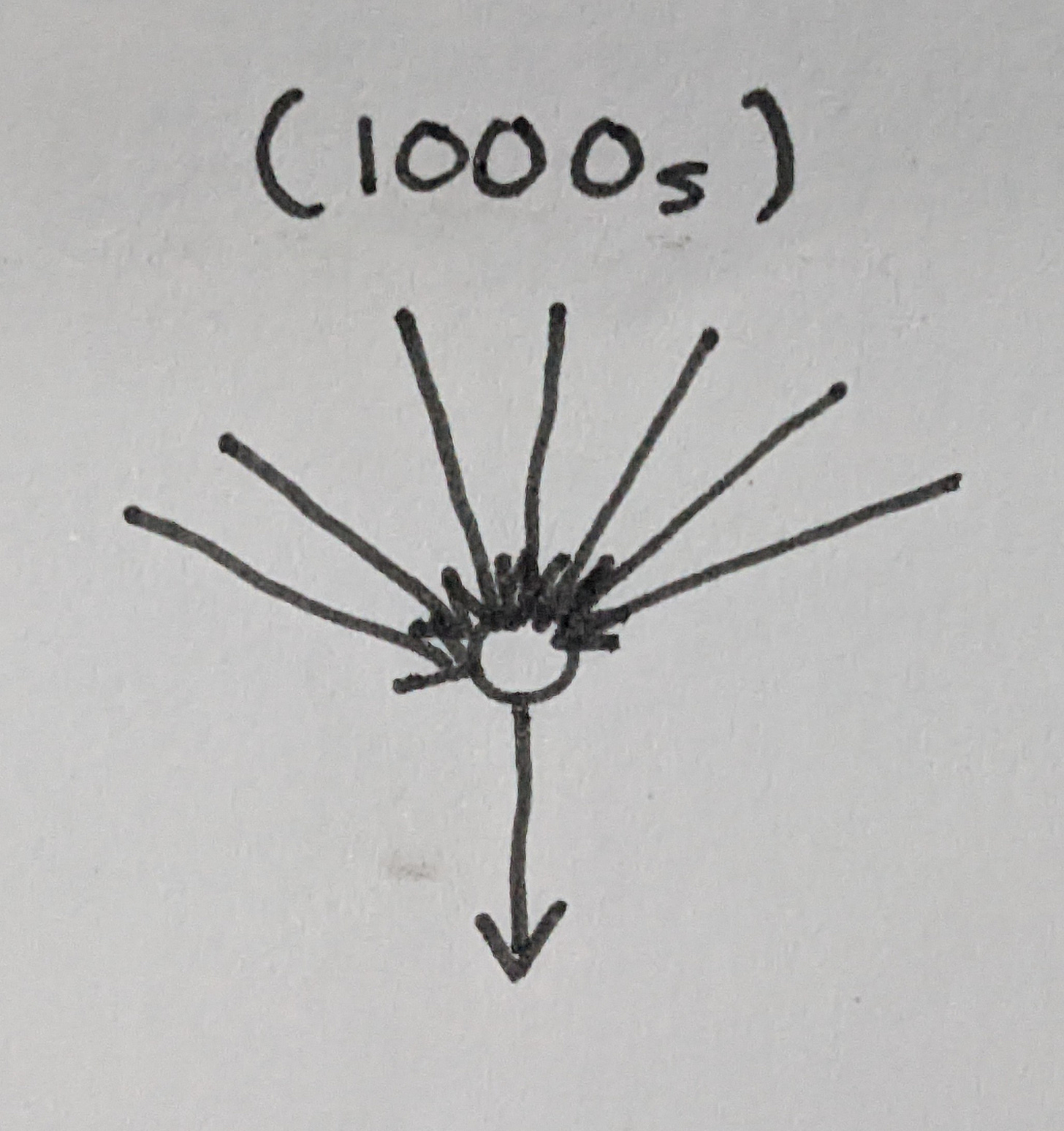
SDM generalizes this notion in a way that we can think of each neuron as encoding not just a single point, but a point with a bubble around it; if the threshold is low enough, many more than just one input point can fall inside it. Further, SDM usually proceeds to give neurons realistic numbers of synapses, in the thousands.
In some sense, the synapses of the neuron correspond to just a point in the input space and the threshold is a measure of how close an input has to be to trigger it, the radius of the bubble.
At this point, we have enough context to understand the name “Sparse Distributed Memory” which refers to this addressing analogy, in the sense that the addresses fill the input space more sparsely than the kinds of dense addressing schemes often used by humans, filling in the gaps with these bubbles.
It's worth noting that it is perfectly possible for these neuron bubbles to overlap, and an input point that falls into the intersection of multiple neurons can cause multiple neurons to fire.
Here, blue bubbles correspond to activated neurons and the yellow bubbles are inactive neurons.
While perhaps multiple neurons firing might seem to increase ambiguity about the location of the input point, in reality it does the opposite. Because the only way for an input to trigger multiple neurons simultaneously is to land in an area where every one of those bubbles overlap, and because the size of that area tends to shrink exponentially with every additional neuron, multiple neurons firing actually allows us to very precisely triangulate the input location to a very small area.
When a neuron fires in the SDM model, hebbian learning kicks in. “Neurons that fire together, wire together.” The neuron makes small adjustments to its synapses so that they more closely approximate the input point. Synapses that got a zero as an input are decremented and synapses that got a one as an input are incremented. Thresholds in SDM stay constant, so the end result is that the bubble moves closer to the input point.
This is illustrated below; this neuron is being pulled toward the white input point, and its bubble is moving closer (red is before, blue is after). A significant amount of overlap exists between the two states (magenta).
One thing that is necessary to make this approach work well is the thousands of synapses on neurons. Attempts to create artificial neural networks, from perceptrons to modern deep learning, generally haven't shown many reasons why large numbers of synapses are really all that necessary. Yet neurons in the brain regularly have thousands.
Perhaps this is just a matter of the brain being a big, flexible neural network that benefits from excessive connectivity. Or maybe the brain just finds adding tons of extra synapses to be cheap enough that it doesn't matter if they provide little extra cost. The math behind SDM however suggests that those thousands of synapses are in fact very useful.
As the weighted sum across these binary inputs is really just a continuous form of a hamming distance function (counting the number of differing bits between two bit vectors), we can look at the statistical properties of hamming weights on large bit vectors.
If we pick a neuron that encodes an N-bit address, and set the threshold of the neuron to allow one bit of deviation (let’s call this variable D), there will be a total of N+1 possible addresses in its bubble. This includes the address itself, plus each of the N addresses that differ by just one bit. When D is 2, this increases to 1+N+(N*(N-1)/2), as now there are only N-1 bits left that can be changed to a point different from the original address.
As we increase D, the volume of the bubble grows roughly exponentially, growing the fastest when D=N/2, and then slowing down before stopping when D=N. The result of this is that the vast majority of points in such a bit vector space are a distance from the address that is close to N/2. However, as N increases, this gets exponentially more true.
Say N=1000 and D=333. This means we're allowing a third of all our bits to be completely wrong and the neuron firing regardless. This sounds like it should be extremely error prone, but some quick combinatorics math shows that, picking a random point out of the entire input space, the odds of landing in this neuron's bubble are about 1 in 10^27.
This is effectively exploiting the weird properties of the “Curse of Dimensionality” for a useful application.
That said, this perhaps shouldn't be that surprising. This idea of encoding things as a bunch of bubbles in a high-dimensional binary space is pretty similar to how error correcting codes work. The main difference here being that ECCs arrange their bubbles into a densely-packed grid with minimal overlap, and then map the closest bubble to an integer encoding, whereas SDM usually uses a much smaller number of bubbles and gives them a lot more freedom to overlap and move around, then encoding the set of all overlapping bubbles.
ECCs also are known to get more efficient as the dimensionality increases, though also often harder to encode/decode.
Now let's explore what happens over time, when an SDM model is given many different inputs.
The state spaces of real-world data rarely explores all possible states, and even more rarely has a perfectly even probability distribution. Any data with any structure worth learning will trace out some complex manifold or other high-dimensional structure that is merely embedded in the higher-dimensional space that is your dataset.
The effect that SDM has is that, as the input point traces out its path through the input space, neurons in SDM are slowly dragged closer until most lie on or near this manifold.
Parts of the manifold that get explored very often may even attract larger numbers of neurons, effectively giving those regions a higher resolution.
At the end, SDM maps out locations along this manifold, outputting a binary encoding of positions inside it. In some sense, it generates something similar to a locality-sensitive hash, as points that are nearby on the manifold are likely to cause similar neurons to fire, creating very similar output bit vectors.
Illustrated here, the manifold traced by the input dataset is the orange region, the orange/yellow is everything covered by neurons, and the blue is the region activated by the white input point. Neuron addresses are black dots. The output vector contains 4 bits that are 1, and the rest 0.
There's a bit more to SDM beyond what I've explored here. For example, there's some mechanisms by which you can implement a kind of sequence memory by feeding the outputs back in as inputs. Toward the end of Kanervi's book, some vague discussion of behavior generation is provided based on learning sequences of cause and effect linked to motor outputs, and then biasing actions associated with desirable outcomes to be played more often than those with negative outcomes.
Wrapping Up
It’s interesting that we're able to get so much out of this model without any differentiability, backpropagation, or many of the other properties that modern deep learning people swear by. That said, SDM is one of the simpler, less accurate, and less interesting models I plan to discuss, and is best thought of as a foundation that many more interesting ideas can be built upon.
In the next part of this series, I'll begin exploring Hierarchical Temporal Memory (HTM), a much more modern theory that expands on SDM with much more detailed and accurate models of neurons and how they connect with each other.
Thank you for reading this Bzogramming article. I’m working on exploring unusual ideas in an effort to push computing toward a more interesting future. If you want to suport this effort and see where I take the ideas in this article, I hope you’ll consider sharing and subscribing.