Undecidability Isn't So Bad
Solving "Impossible" Problems
Undecidable problems in computing are generally considered impossible to solve, and many lament that this means that many of the wonderful code analysis tools that we might wish for to automatically detect all the bugs in our code simply cannot be built, even in theory. In reality however, this is not entirely true, and really just boils down to a misunderstanding.
For example, Alan Turing’s original proof on undecidability shows that if we had a computer that could, for any given program and any input to that program, produce a perfectly accurate prediction of whether that program loops forever or if it eventually halts, that this machine would create a mathematical contradiction. Therefore, it cannot exist. This is often assumed to mean that answering such a problem is entirely impossible, but there is no reason at all why this would apply any less to the human brain than it would a computer algorithm. With that in mind, ask yourself, does the following loop halt?
while(true){
// twiddle our thumbs
}
This isn’t a trick question or anything. To anyone with a basic understanding of code, this is an obvious example of an infinite loop. Has your brain just violated mathematical law? Have you just proven that the human brain is not a computer but instead something magical? Nope, absolutely nothing of the sort, you’ve simply shown that the common narrative around what undecidability means isn’t very accurate.
If you dig into the details of Turing’s paper, you find at its core a diagonalization argument, which is just a method for showing that one set must be bigger than another. His argument really just boils down to a proof that the set of all possible program states which encode proofs of properties of other program states is smaller than the set of all possible states.
You actually can attempt to build a program that tries to answer undecidable problems. One trivial method would be to simply run the input program until it halts, and then report it as having halted. Another method might be to track all of the states that an input program can reach, and to look for loops or repeats. Plenty of other creative tricks can be devised as well, but inspecting the failure cases is interesting. Ignoring the fact that many of these algorithms could easily be hopelessly intractible to actually run because of how vast even very small program state spaces are, what we find is that any program we think of must either sometimes give a wrong answer, or the loop-detecting program itself will ironically get into an infinite loop.
We can in fact build a correct, approximate undecidability solver if rather than insisting that our loop-detecting program always return YES or NO, it can also sometimes return IDK. Technically speaking, returning “I don’t know” for every possible input is correct, albeit not very useful. Reducing the number of IDK cases to zero is impossible, but correctly answering in at least a subset of cases is certainly not.
And of course, halting is only the classic example of an undecidable problem - really detecting any nontrivial property of a program’s behavior is undecidable, per Rice’s Theorem.
Humans generally design software that is meant to be understood. If our programs truly contain a lot of properties that are impossible to verify, that’s often a good indicator that there is a bug in the code somewhere.
“Here Be Dragons” Analysis
There’s a method I like to apply to studying difficult problems which I call “here be dragons” analysis. The basic idea is to divide things up into a number of distinct cases which you may or may not be able to say useful things about. If you can show that many of these cases are well-behaved, you can show that the badly behaved ones must have or lack certain properties related to how you divided things up.
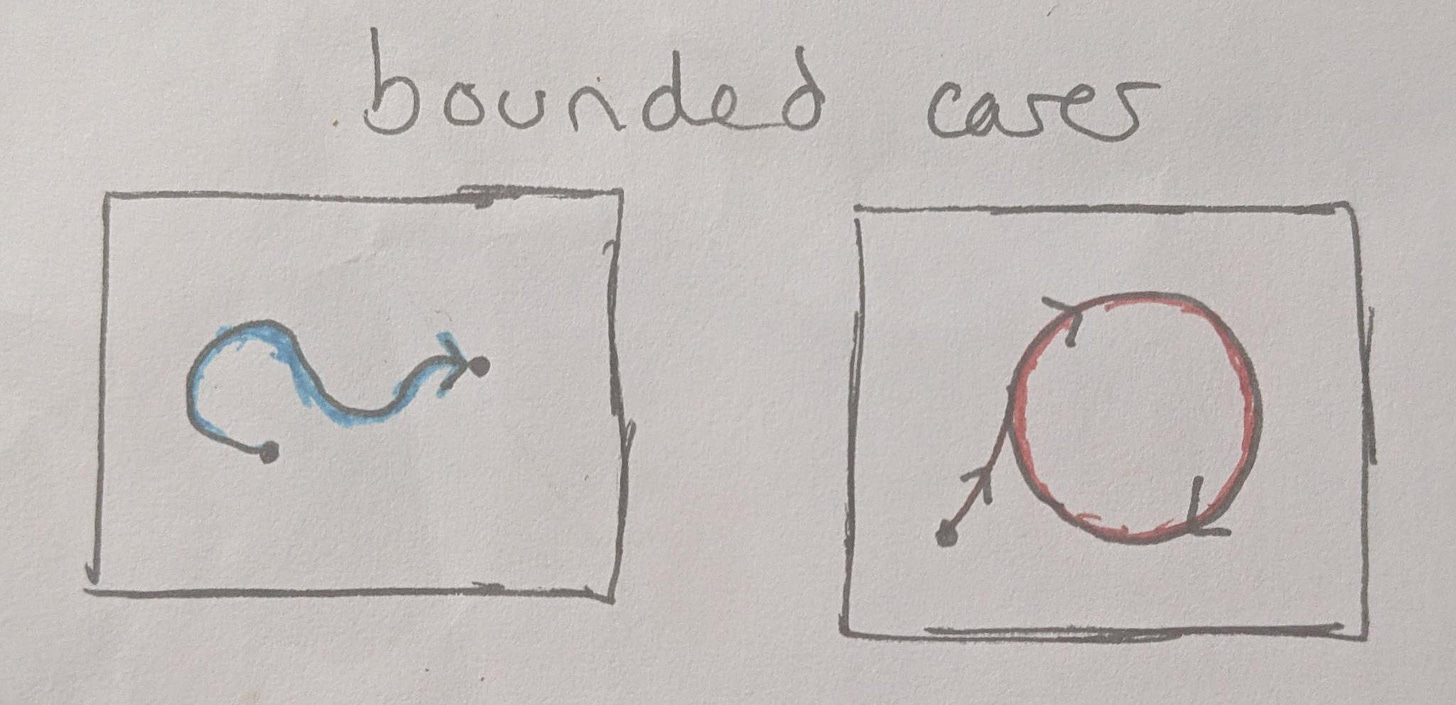
Let’s say we know something about our program, namely that it fits into a finite amount of memory. Finite memory implies a finite statespace, and therefore at least in theory the entire state space can be enumerated (even if this is too costly in practice). Therefore, this situation is actually decidable. If we have a powerful enough computer and enough time, we can trace out any path through the state space and look for cycles and guarantee when a program does or does not loop forever. Therefore, the truly undecidable problems cannot be programs that fit neatly into a finite amount of memory. They must in fact grow forever!
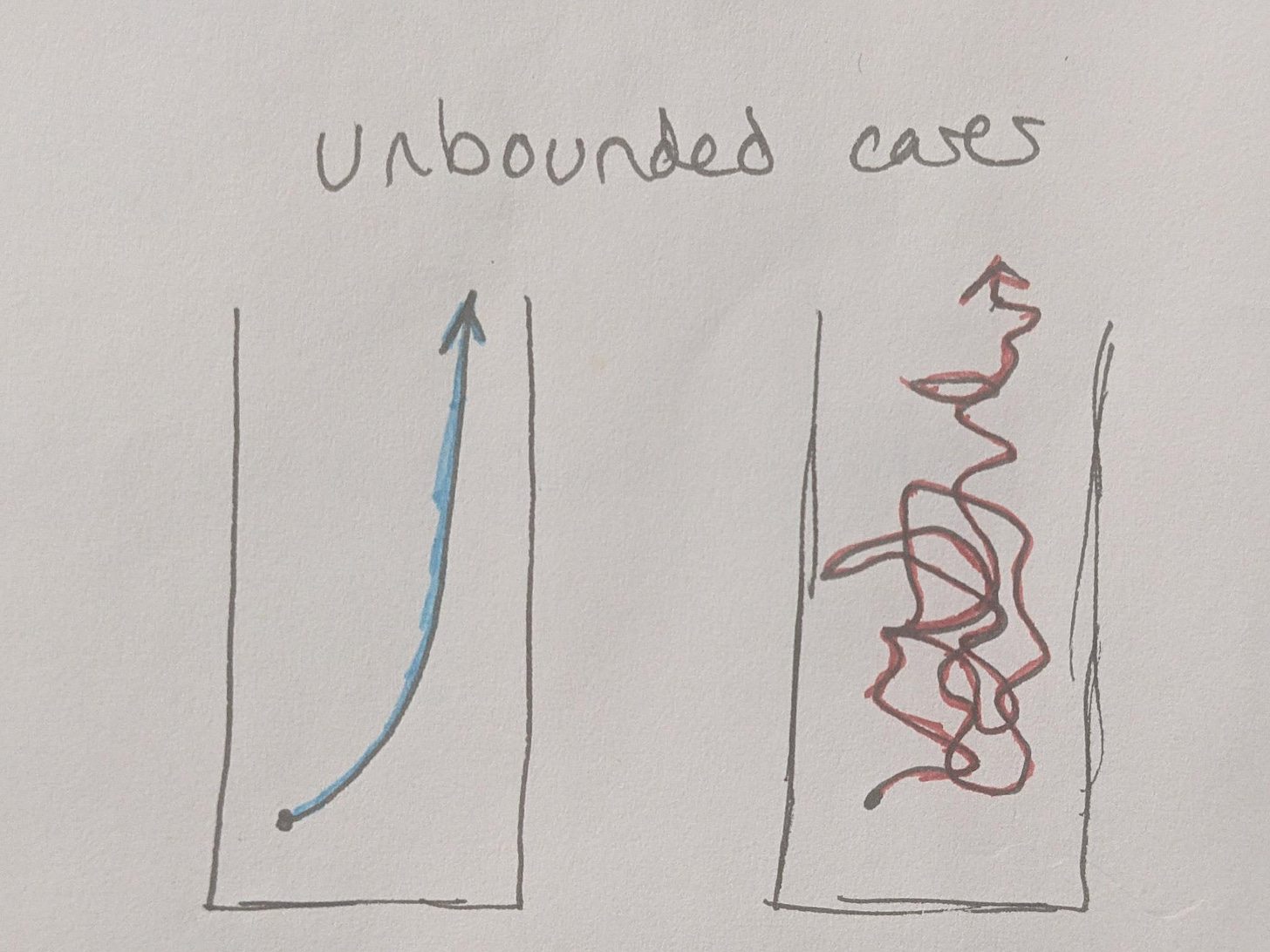
Then we can look at the unbounded cases. If we have a program that simply expands in a simple way, we might be able to figure out some clever analysis that determines the rule that it follows and show that it grows without bound. This is another case where the program fails to halt, albeit one where the program doesn’t so much get caught in a loop, but where it simply grows forever.
Then there’s another case - one where the program jumps around through some statespace without much of a pattern, but gradually expanding to larger and larger memory requirements without an obvious limit. If we cannot devise some analysis to detect a pattern here, then how can we tell if the program is spiraling off into chaos or if it eventually repeats without simply waiting a potentially infinite period of time for it to retrace its steps?
This unbounded chaotic expansion case is therefore the one case where we cannot show that the program eventually halts, and therefore every program which is truly undecidable must behave like this - jumping around without an obvious pattern while slowly (or rapidly) expanding its memory footprint. Granted, as mentioned before, there are a great number of cases that may be theoretically decidable which in practice are too expensive to verify.
One particular implication of this, albeit one that may not be appreciated by mathematics enthusiasts, is that in many respects the famous Collatz Conjecture is a good example of a problem which seems to fall into this potentially-undecidable case. Its inputs jump around chaotically, sometimes shooting up very high before dropping back down. Despite being a shockingly simple problem, it stubbornly refuses to yield to any kind of mathematical analysis.
In fact, at one point John Conway even proposed FRACTRAN - an esoteric programming language designed around a generalization of the Collatz Conjecture that is Turing-complete. So we know that it’s not hard to generalize Collatz into something that is provably undecidable in at least some cases.
Hierarchy Theorems
Beyond simply doing some trickery with diagonalization, Turing’s original proof of the undecidability of the halting problem relied on another interesting detail; self-referentiality. The specific example case that was shown to be undecidable is when a halt-detection program is asked to answer questions about a slightly modified version of itself, augmented to return the opposite of its. The specific way in which this is done results in a variation of the liar’s paradox, where the program is caught lying no matter what it answers.
Pinocchio Paradox : Pinocchio proclaims “my nose grows now”
The consequence of this is that many provably undecidable problems boil down to computers attempting to prove things about themselves. These are not the only cases which are undecidable, but just some of the simpler cases to prove.
However, we can actually get some valuable intuition for what’s going on here by looking at the Time Hierarchy Theorems, which are in effect a finite version of Turing’s proof.
The THTs look at what happens when we restrict computers to be able to run only for a finite amount of time. The analogue of the halting problem here is asking whether or not a program finishes running before a certain time limit. If we have any question we wish to ask about the behavior of a program beyond simply what it outputs when we run it, then doing so requires adding some amount of additional work that must be performed. This work is not free, and increases the runtime of our program. As a result, many possible programs that could run on a time-limited computer and finish close to the limit will, given some additional overhead, fail to finish before the limit. If we wish to answer our question for every possible program that can be run on our time-limited computer, we cannot do so unless we are given a computer with an even longer time limit, enough to account for the full time limit of the first computer plus the overhead for our specific question about it.
Put in simple terms - to be able to answer questions about every possible way in which a computer could behave, we need a computer that is fundamentally even more powerful.
The way I like to intuitively frame this is that the Time Hierarchy Theorems are the actual rule about how undecidability works, and that Turing simply proved a few decades earlier that the THTs don’t stop applying even when we have an infinitely powerful computer. Answering questions about an infinitely powerful computer, where programs could run for an infinite amount of time, requires more than an infinite amount of computing power, which is why the diagonalization argument involves both countable and uncountable infinities.
Implications
So if undecidability in fact is not actually so bad, then perhaps we should stop using mathematical impossibility as an excuse for why we don’t have better development tooling.
The truth is that actually a great deal of sophisticated static analysis is already done inside the guts of many modern optimizing compilers in order to determine which optimizations are and are not safe to apply. Those decisions require some sophisticated understanding of how code behaves. The methods outlined in this article are very general-purpose, but not very practical or efficient, whereas plenty of static analysis work has been done to find methods that are more useful, at least for the kinds of programs humans tend to write.
The problem is that this is largely designed to be some invisible black box applied during compilation, largely invisible to the programming language or the human. Perhaps that’s something we should be rethinking.
This has been a relatively short article tonight, on a subject that I’ve referenced a number of times but had been meaning to get around to addressing directly. I’m trying to write a bit more often, and honestly I have a backlog of interesting articles that I’ve been meaning to write for a while that I should just get out.
I have also been busy with other work, and that usually takes priority.