Programming in Hyperspace pt 1
[A repost from my old Medium blog]
This article is a repost of an article I wrote on Medium in 2019. Part 2 will be posted later this week. This is perhaps a little more rough around the edges than more recent writing of mine, but it’s one of my more interesting works from my old blog, and part 2 especially gives some useful background and geometric intuition that should prove very useful for the next couple entries in my Neural Computing series.
There are also some loose threads and unresolved problems I mention across these two articles that I have found some more satisfying answers to in the past 3 years, which I’ll probably write about here eventually. I have quite the backlog.
Enjoy!
Imagine programming as a type of problem, akin to a maze meets an obstacle course. You start at point A, an empty text file, and you need to get to point B, a finished, working application. Along the way, you’re met with many decisions, never certain which direction is best, and you frequently find yourself at an obstacle that must be overcome.
Perhaps you know the general direction to head, and have a few rules of thumb to make educated guesses. Perhaps you recognize some of these obstacles, and armed with prior experience, can confidently overcome them. Perhaps you even know how to find a few rabbit holes and secret passages, allowing you to sneak around an otherwise difficult obstacle with ease.
At your side, you carry your trusty toolbox, with everything you need to get around; you have your data structures, algorithms, and a few mathematical tools and functions. Of course, all your tools are composite; they are built from smaller tools, and often those are made of yet smaller tools. At the bottom of it all is the most fundamental tools; control flow, random memory access, and arithmetic. Everything else is just fancy combinations of these basic components.
You come across an obstacle. You have some options here. You can go left or right. You can try to scale it and go over. You can try to dig underneath. You can perhaps even attempt to plow straight through (brute force). All these basic options may be analogies for simple tools. If you’re wandering through some great labyrinth or making your way through some mathematical swamp, things may be harder, more complex. So you bust out the more complex tools for those — as you need a more complex path to get through such places.
But you recall that time you read about higher dimensions. Or that time you read Flatland. Or that time you tried reading that Stephen Hawking book, specifically the chapter on wormholes. Or that time you spent a weekend trying to learn machine learning, and attempted to grasp the idea of thousand-dimensional gradient descent. You wonder, is there another way to pass this obstacle? Is there some other direction I could take?
With every new dimension comes a new set of directions. In one dimension, you have left and right. In two, you gain up and down. In three, you gain forward and backward. With every new dimension, you gain more freedom to find your way around obstacles. So you ask yourself — what if you could take a step into hyperspace, into the fourth dimension, and find a shortcut along the way, via some new, mind-bending direction?
We can take a look through any CPU’s instruction set, and start looking for new tools. At first, we find all the obvious stuff — arithmetic and comparison operations, branch instructions, and load/store operations. Simple stuff. Then there’s some more sophisticated stuff; atomic and vector operations for working with parallelism, and interrupt management for working with the operating system, devices, and exceptions. Technically different stuff, but not fundamentally different.
Then you come across the arcane and strange tools of the Bit Wizards; AND, OR, XOR, NOT, SHIFTs and ROTATEs. Maybe you recognize those a little. Then you come across CTTZ, CTLZ, and POPCOUNT. And you wonder to yourself, is this what you’re looking for? Are the secrets of the fourth dimension hidden in these tools?
Just some quick context before we proceed here
I’ve been working on a quite ambitious programming language, on and off for the past couple years. It’s called Bzo. I won’t go into a long list of everything that’s planned for it here, but I will mention one insight I’ve had.
If you are offering developers nothing but the exact same set of tools they’re already accustomed to, just with a fresh coat of paint, then you’re not providing anything really valuable.
So I’ve been thinking about what I can provide in Bzo that will be unique, and different. The rest of this article is devoted to my exploration of bitwise programming, which is (among many other things) one of the “new tools” I want Bzo to provide (though few of these are actually “new”, rather just uncommon).
Note: This article is split into multiple parts, as it was getting quite long. I’ve saved the most exotic stuff for part 2, though perhaps you might consider some of the stuff here to be exotic too.
Classic Bit Manipulation, and the Sheer Power of Your CPU
I’ll assume from here on out that readers will already be familiar with the basics. AND, OR, XOR, NOT, SHIFTs, and ROTATEs. Those, and how numbers are encoded. If not, here are a few simple videos on the subject that should introduce them well:
Note: “Circular Shifts” and “Rotates” are the same thing.
CTTZ, CTLZ, and POPCOUNT
Also, a few operations not mentioned are CTTZ, CTLZ, and POPCOUNT. CTLZ and CTTZ are “Count leading zeroes” and “Count trailing zeroes” respectively. They count the number of contiguous zeroes at the beginning/end of a number. For example:
CTTZ(00101000) = 3
CTTZ(10110000) = 4
CTTZ(00000111) = 0
CTLZ(00011010) = 3
CTLZ(00001101) = 4
CTLZ(11001100) = 0
These can be used for, among other things, figuring out the index of the highest/lowest set bit.
POPCOUNT counts the number of 1 bits in a number. For example:
POPCOUNT(00000000) = 0
POPCOUNT(00010000) = 1
POPCOUNT(00100111) = 4
POPCOUNT(11111111) = 8
This can be useful for a variety of calculations. Bitsets can utilize this for counting the size of the set, or the number of overlapping bits between two bitsets. There’s more that we’ll see in part 2 as well.
Performance
A typical integer on a 64-bit machine will take up 64 bits. In other words, that tiny piece of data that takes up a minuscule 8 bytes of RAM is an array of 64 boolean values. 64 of them. That’s pretty densely packed data.
Not only is it dense though, but your CPU can operate on all of those boolean operations in parallel. In a single operation. And, a bitwise operation is just about the fastest and most efficient operation your CPU can do.
Then you can take into account vector operations. AMD’s upcoming1 Zen 2 CPU architecture will have 4x 256-bit vector pipelines per core, and will scale up to 64 cores per CPU (for server models). Run the numbers, and that’s 65536 boolean operations per clock cycle. If the CPU runs at just 2 GHz, that’s over 131 trillion boolean operations per second. On a single CPU.
These operations are insanely fast and powerful, if you know how to use them.
More Sophisticated Bit Manipulation
This next section is full of number theory -type stuff, and is full of weird things you can do with multiplication/division/modulus on bit vectors. Perhaps it’s not extremely useful (though I find myself using these kinds of tricks occasionally), though it is something good to have in your toolbox when doing low-level programming. There may even be some unique applications for some of this stuff.
Note: Many of the examples in the next few sections rely heavily on the arrangements of digits/bits, so I’ve added extra spaces, horizontal bars (|) and zeroes into the numbers to emphasize these.
Multiplying Bit Vectors
Because multiplication is just repeated, shifted addition, we can use multiplication to perform a large number of addition and shift operations in a single operation. If we can line up our numbers in a way that we know that bits won’t overlap during the addition process, then the adds turn into OR operations.
In much the same way that 11 * 3 = 33, 111 * 3 = 333, and 001 001 001 * 15 =015 015 015 in decimal, we can do similar tricks with multiplication in binary.
A few simple binary examples (more in the following diagram):
001 001 * 011 = 011 011
001 001 * 101 = 101 101
Multiplication for Horizontal Addition
We can also use multiplication to perform horizontal adds; partitioning numbers into groups of bits/digits, and then adding up partitions. An example in decimal would be 01 01 01 * 03 04 05 =
00|00|03|04|05 +
00|03|04|05|00 +
03|04|05|00|00 =
03|07|12|09|05
If we want to add up each partition (03, 04, and 05), we can see that the middle column in the example contains this sum. This all relies on our numbers in each partition not being too large as to carry digits into other columns. To get the column we want, we can apply a little bit of shifting and masking. Note that some of these columns may be lost due to overflow.
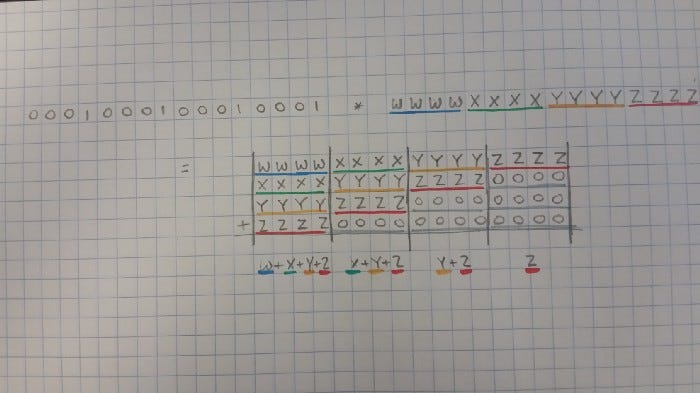
Once again, we can adapt this into base 2:
0001 0001 0001 0001 * 0011 0010 0100 0101 =
0000|0000|0000|0011|0010|0100|0101 +
0000|0000|0011|0010|0100|0101|0000 +
0000|0011|0010|0100|0101|0000|0000 +
0011|0010|0100|0101|0000|0000|0000 =
0011|0101|1001|1110|1011|1001|0101
The middle column is the full sum.
Division and Modulus as Bitwise Operations
As if things couldn’t get crazy enough with using multiplication for bit manipulation, we can use division and modulus as well! (Specifically, the unsigned integer versions)
The simplest case here is using them as an inverse of multiplication. If we can create repetitive patterns in bit vectors with multiplication, we can use division and modulus to detect and extract those patterns!
An example in decimal would be the inverse of one of the above examples. 333 clearly has a repetitive pattern. We can represent that pattern with the number 111, and divide 333 by 111 to test it. If the remainder is zero, we have a match, and the result of a division will give us the repeated pattern. If we search for a pattern that does not exist, we will get a non-zero remainder, and the modulus operation will alert us that our pattern detection has failed.
We can do the same thing with more complex patterns, for example 1501515 / 100101 will match as a pattern, and will return 15 as the repeated value. Because multiplication is commutative, we can also solve for the pattern by searching for the value. 1501515 / 15 = 100101.
Once again, all these fancy number theory tricks work in any base, including binary. So feel free to use it for bit tricks (though maybe keep this stuff contained, or in your own private projects rather than confuse your coworkers with tricks like this!).
Modulus for Horizontal Addition
Modulus can also be used for horizontal adds. I won’t go into the math behind this, but if you know a little number theory, you can probably figure it out yourself. Once again, this works in any base, so we can use examples in base 10 and generalize to get base 2 versions.
1 2 3 % 9 = (1 + 2 + 3) % 9 = 6
04 05 06 % 99 = (04 + 05 + 06) % 99 = 15
In binary now:
0011 0101 0001 0010 % 1111 =
(0011 + 0101 + 0001 + 0010) % 1111 = 1011
If we want to split the bit vector into N-bit blocks and add them, we take the bit vector mod ((2^N) - 1).
Unfortunately, modulus is actually quite an expensive operation and horizontal adds can be more efficiently done with some shifts and adds. You can still do this trick, but most optimizing compilers are aware of it, and will often optimize it to an implementation that does not involve modulus.
Why?
Perhaps if you’re doing some fancy bit manipulation, some horizontal adds might come in handy. Creating repeating patterns can occasionally be useful too (I sometimes find myself using it in my code), but I have a feeling it could have some minor applications somewhere else. Perhaps Digital Signal Processing or Compression?
Exploiting Density
A single byte can store 8 bits. 8 boolean values. If your CPU supports 256-bit vector units (as most these days do), you can fit a whopping 256 bits into a single CPU register. So what can you do with 256 bits?
Well, there are 2⁸ possible values that can be stored in a single byte. That’s 256. So, you can store 1 bit for each possible value of a single byte. What can you do with this?
Say we’re parsing some text. For the sake of simplicity, let’s assume it’s all in ASCII, so 8 (or technically 7) bit encoding. If we want to test if a particular string contains say, only lowercase letters, we can reduce this to just a lookup in a bit vector; a couple of bit shifts, an AND op, etc. There are probably even ways of vectorizing it for better performance.
In fact, we can pick any set of possible values for a byte, and easily generate a simple 256-bit value to represent it. We can then do fast lookups on that and use it as a filter for even complex patterns.
Suppose we take two pieces of text, and want to know the set of all characters they have in common? We can build up small bitsets of all the byte values that appear in each, and compare them with AND, OR, XOR, etc.
All of this is WAY faster than doing these kinds of operations on complex data structures full of pointers, and algorithms full of branching logic and loops.
Exponential Space?
Technically, all this takes exponential space. Typically, anything exponential causes programmers to run away in fear. In reality, everything has some value at some point. Exponential algorithms can actually be surprisingly useful in small, simple cases where overhead is low, especially because they are often much simpler than more “efficient” algorithms.
In fact, I’d argue that “inefficient” solutions can often be better than “efficient” solutions, mainly because that efficiency often comes with increased complexity, most often in the form of control flow and memory access, both of which can be incredibly expensive if they aren’t easy enough for the CPU to predict. But that’s a worthy of a whole other article. Perhaps many.
Analysis on the Structure?
There’s a lot more to this I think. Stuff with analyzing this kind of structure. It’s something I’d like to investigate more before I’m really ready to talk extensively about it. So instead of saying more, I think I’ll just leave one of my all-time-favorite talks here. Perhaps it’ll give you an idea of where the potential I sense in this is.
“Quantum” Finite Groups
Group theory is a pretty heavily-researched area of mathematics. Groups are abstract mathematical structures that show up in everything from modelling rotations to theoretical physics.
Suppose we have a finite bit set, say 64 bits. We can treat it as a number range mod 64. Let’s say we then set a single bit. We can think of this as storing a single integer set to that index. If we want to add/subtract with that number, we can rotate it left or right.
An addition-like operation is technically all we need to be considered a group.
However, if we set more than one bit, we suddenly find that we’re performing this operation on multiple values in parallel.
We can also create a variation of this where we can add multiple values in parallel. This can be done by ORing together the results of multiple rotates. In fact, if we had an operation in a CPU that was similar to a multiply, but performed rotates rather than shifts, and ORs rather than adds, we could easily have cheap hardware acceleration for this.
We also could throw in other bitwise operations, like AND, OR, NOT, and XOR for filtering, combining, and comparing these sets of values.
As a result, we can add/subtract numbers in a small finite group, simulating many of these operations in parallel. In a sense, we’d be doing something a little like the [flawed] pop-science description of quantum computing of simulating every path through a calculation in parallel. It’s quite limited in terms of scope, but perhaps there’s some interesting research to be done by going further down this rabbit hole.
Upcoming in Part 2…
Stay tuned for part two, where we’ll be getting into the really exotic stuff; Sketches, Shadows, and Locality-Sensitive Hashing. In other words, the places where bitwise operations, constraint systems, machine learning, computational neuroscience, and more all meet.
Thank you for reading this article, part 2 should be out later this week, or if you’re really impatient you can go read it on Medium (note: I don’t post anything there anymore, you don’t need to follow that account).
I was planning on writing the next installment of my Neural Computing series, but I’m too tired tonight and there’s a lot more math I need to brush up on than I thought. Don’t let that scare you off, it’s actually not that hard to conceptually understand, there’s mostly just a few fine details I want to get right.
If you’re new here and want to follow my work, you can follow below. Sharing my work and getting a paid subscription are also greatly appreciated!
Zen 2 has since been released. In fact, I’m writing this on a laptop with a Zen 2 CPU.